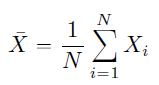Measures of variability tells ‘how spread’ out is the data. How far values are from the mean or median. Here, we’ll be discussing 6 common types of measures of variability which are:
- Range
- Interquartile Range
- Mean Absolute Deviation
- Variance
- Standard Deviation
- Median Absolute Deviation
Let’s see these in detail. We’ll be using ‘iris’ dataset for the examples which is built-in dataset in R.
- Range
We can calculate range as largest value minus the smallest value.
#Range of Sepal.Length column
#1. Using without function
max(iris$Sepal.Length) - min(iris$Sepal.Length) #Output: 3.6
#2. With function range() - It gives both the largest & smallest value in a vector
range(iris$Sepal.Length) #Output: 4.3, 7.9 Note! Range is not a good measure of variability as it is highly influences by outliers. If a dataset has some extreme outliers, we’ll get totally different range.
2. Interquartile Range
IQR is like a range but it calculates the difference between the difference between 25th & 75th quantile. It is basically the middle half (50%) of the data i.e. one quarter of the data falls below the 25th percentile & one quarter of the data is above the 75th percentile, leaving the “middle half” of the data lying in between the two.
Quantiles(most commonly called percentiles). Eg. 10th percentile of a dataset is the smallest number (x) such that 10% of the data is less than x.
Median of a dataset is at 50th quantile/percentile.
#Find 50th quantile/median of Sepal.Length column
quantile(iris$Sepal.Length, probs = 0.5) #Output: 5.8
#Median of Sepal.Length
median(iris$Sepal.Length) #Output: 5.8
#Find 25th & 75th perceentile of Sepal.Length
quantile(iris$Sepal.Length, probs = c(0.25, 0.75))
#Output: 25%:5.1, 75%:6.4 Hence, IQR= 6.4-5.1=1.3
#Find IQR using function
IQR(iris$Sepal.Length) #Output: 1.33. Mean Absolute Deviation
Mean Absolute Deviation is a measure of average of the absolute deviation between each observation and the mean.
We use absolute here because we’re just interested in how ‘close’ it is to the mean doesn’t matter if the value is higher or lower than the mean
Formula to calculate Mean absolute deviation is:
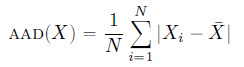
##Find Mean absolute deviation of Sepal.Length column
#1. Without function
data<-iris$Sepal.Length
mean<-mean(iris$Sepal.Length)
dev<-abs(iris$Sepal.Length - mean)
mad<-mean(dev) #Output: 0.687
#2. Using aad() function in lsr package
aad(iris$Sepal.Length) #Output: 0.6874. Variance
Variance measures how far/spread out each data point is from the mean. Formula of variance is:
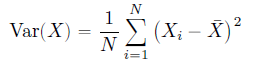
This formula is very similar to Mean Absolute deviation, here we just use squared deviations instead of absolute deviation. That is why sometimes Variance is also called ‘Mean Squared Deviation’.
One explanation of why we use squared deviation in variance is if variance is less , it means on an average every value has a low difference with the mean. and hence, we can conclude that all the values are approximately close to the mean. However if the variance is high, then we can understand there are lot of extreme values in the dataset.
Note! Variance is additive i.e. let’s say there is a variable X with Var(x) & variable y with Var(y), then we can create a column Z where:
Var(z)= Var(x) + Var(y)
#Variance of column Sepal.Length
var(iris$Sepal.Length) #Output:0.685Now in R, instead of averaging the squared deviations where we divide by N, R chose to divide by N-1 i.e. R uses below formula for variance:
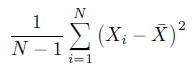
We divide by N-1 instead of N because we define Variance(s²) in a way such that it is an unbiased sample variance.
Variance with a divisor of N-1 is a variance calculated from the sample as an estimate of the variance of the population from which the sample was drawn. Variance which is calculated using deviations from the sample mean underestimates the desired variance of the population. Using N-1 instead of N as the divisor, corrects for that by making the result a little bit bigger.
When sample is the whole population, we use N as a divisor because then mean is population mean not sample mean.
Note! Variance is not interpretable, one reason is since its squared so it’s unit is not same as the unit of the dataset. That is why instead of variance, people prefer to use Standard Deviation which we will cover now.
5. Standard Deviation
Standard deviation is the square root of the variance. It is more interpretable because it is expressed in the same units as the data (i.e., values, not squared values).
Eg. Suppose there are two grocery delivery apps, both advertise 20 minutes average delivery time. Now, let’s say App 1 has a SD of 10 minutes and App 2 has an SD of 5 minutes. Now we can understand, App 1 with larger SD has more variable delivery times and a broader distribution curve compared to App 2 with less variability, so we’ll choose App 2.
- Small standard deviation indicates that the data points are closer to the mean i.e. values in the dataset are consistent.
- While high standard deviation means data values are spread out further from the mean, they become more dissimilar and extreme values become more likely.
Formula of sample standard deviation is:
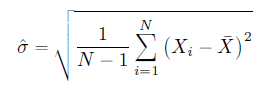
#Find SD of Sepal.Length column
sd(iris$Sepal.Length) #Output: 0.828Note!
- If a distribution is normal, symmetric or bell shaped, then in general 68% of the data fall within 1 standard deviation of the mean
- 95% of the data fall within 2 standard deviation of the mean
- and 99.7% of the data fall within 3 standard deviations of the mean.
6. Median Absolute Deviation
Median Absolute Deviation is similar to Mean Absolute Deviation, instead of mean, it used median.
Eg. In an iris dataset, the median Sepal.Length is 5.8. However, there is some amount of variance in the dataset. The MAD value is 0.7, indicating that a typical Sepal.length would differ from the median value by about 0.7 points.
#Find Median Absolute Deviation of Sepal.Length column. Default value of constant = 1.4826 which relies on assumption that data is symmetric & follows normal distribution.
mad(iris$Sepal.Length, constant=1) #Output: 0.7Thank you for reading.
References: