A measure of central tendency is a summary statistic that represents the center point of a dataset. It indicates where most values in a distribution fall. In this blog, we will see the basic definitions of mean, median & mode and see how to calculate these in R.
There are broadly 3 types of measures of Central tendency:
- Mean (Sometimes, people also use Trimmed mean)
- Median
- Mode
- Mean
The mean of a set of observations is just an average: add all the values and then divide by the total number of values.
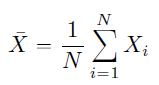
Let’s see how we can calculate mean in R. We are taking an example of ‘iris’ dataset here which is a built-in dataset in R.
##Calculate mean of Sepal.Length column. We can either calculate mean without function or with function mean()
# 1. Without function
sum(iris$Sepal.Length)/length(iris$Sepal.Length) #output: 5.84
# 2. With function
mean(iris$Sepal.Length) #output: 5.84Trimmed Mean
Mean is highly sensitive to outliers, therefore if in a dataset there are some extreme values present, mean is not a good measure of tendency. We can either use Median or Trimmed mean. First let’s see what trimmed mean is.
To calculate trimmed mean, we discard the extreme data points from both the ends(i.e. the largest & smallest) and then take the mean of rest of the data.
We describe trimmed mean in terms of %. So, a 10% trimmed mean will discard the largest 10% of the data & smallest 10% of the data and then takes the mean of 80% of the remaining data.
Let’s see how to calculate trimmed mean in R
data <- c( -15,1,6,4,7,8,4,5,9,12 )
#find 10% trimmed mean (10% trim from both sides)
mean(data, trim = 0.1) #output: 5.52. Median
The median of a set of observations is the middle value. It is the value that splits the dataset in half.
- To find median, sort the data in ascending order
- In case of odd no. of observations, median is the middle value.
- In case of even no. of observations, median is the average of 2 middle values.
Outliers has a small effect on median since median doesn’t depend on all the values in a dataset.
Income is the classic example where we should use median instead of mean. Because if income of some wealthy person is also added in the dataset, mean will overestimate where most of the household income falls.
Let’s see how to calculate median in R.
#Find median of Sepal.Length column
median(iris$Sepal.Length) #Output: 5.83. Mode
Mode is the value that occurs most frequently in a dataset. If no value repeats, there is no mode in the dataset. And if there are multiple values that occurs most frequently(same no. of times), then it’s called multimodal meaning data has multiple modes.
Let’s see how to calculate mode in R. Since core packages in R don’t have function for calculating the mode, we will use the package ‘lsr’ which has functions to calculate mode.
#Load package lsr
library(lsr)
data<-c(2,2,3,4,5,2,3,2,3,2,3,2,3,4,5,4,4,4,5,6,6,6,1,1,1,1,1)
#Find mode
modeOf(data) #Output: 2
#Find frequency value of the mode
maxFreq(data) #Output: 6Note! When to use mean, median or mode
- In a symmetrical continuous data, mean, median and mode are equal. Here, mean is preferred since it considers all the data points in a dataset.
- If a distribution is skewed, median is preferred.
- For ordinal data, median or mode is preferred.
- For categorical data, use mode.
Thank you for reading 🙂
References:

Leave a Reply